为什么量子力学的发展总是伴随着疑惑和争论？这个问题要从量子力学的源头-黑体辐射讲起，这篇文章将会用用最通俗的语言把这个问题剖析清楚，争取让中学生也能听明白。

这篇文章主要讲述几个问题，一，为什么普朗克公式与实验数据符合？二，维恩公式为什么在长波波段低于实验值。

所谓黑体，指的是不反射电磁波的物体，所有射向黑体的电磁波都会先被黑体吸收，其能量再全部以电磁波的形式辐射出来，也就是从它表面出去的光全都是它自身发出来的。这里要补充两点，一，高纯净的玻璃也几乎不反射电磁波，因为光线都透射过去了，所以黑体的概念又补加了一条，既不能反射，也要做到不能透射。二，能量要全部以热辐射的形式散发出去，这里又隐含了一条，不能热传导。黑体的周边应该是真空环境，否则很难杜绝热传导。 早期黑体辐射实验如下图所示。

（左图） Lummer和Pringsheim使用的辐射计。辐射计基于热测量，入射的光被接收的金属片吸收，被加热的金属片的电阻由Wheatstone电桥精确测量。据说其温度分辨达10-7 K {曹：我对此说法存疑}。（右图）Lummer和Kurlbaum 制作的电加热黑体辐射源。

选自中科院物理所研究员曹则贤的文章《黑体辐射公式的多种推导及其在近代物理构建中的意义(一) | 贤说八道》

在黑体这个研究对象确定之后，接下来就是要测量了。单位面积上的黑体表面，比如一平方厘米，其所发出的电磁波是混杂的，可以说包含了电磁波的全部频段，各个频率各个波长的都有。

人们要先将黑体表面发射出来的这些混合光分离开来，分成单色光，再用辐射计去接收单色光，继而测量得到该单色光的辐射功率。分离的原理并不复杂。类似于三棱镜分离。如下图所示。

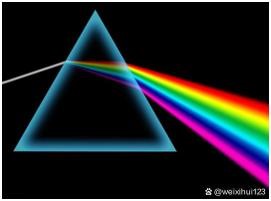
最后，人们将实验测量的十几个甚至几十个数值用曲线连接起来，就得到了该温度下的辐射曲线。横轴可以用频率表示，也可以用波长表示，两者互为反比，频率大，则波长短。频率小则波长大。纵轴表示单位面积上的某单色光的辐射功率，又称单色辐出度，单位是W/m²。记住是单位是W/m²。

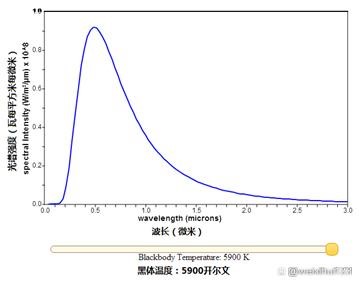
黑体辐射的研究，简单来说就是物体吸收能量后自身发光，发出混色光，人们通过技术手段把这些光筛分成单色光，再分别测量这些单色光的功率，把这些测量值连接起来得到的辐射曲线，就是该温度下物体的辐射规律。事实上，辐射只和温度有关，而和材质无关，300度烧红的木炭和300度烧红的铁球，辐射曲线是一样的，都遵循同样的规律。1896年，德国物理学家维恩先生得到了一个公式，很好的描述了这个规律。下图是该公式。

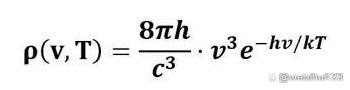
另外，从这条曲线可以看出，辐射功率随着波长（或者频率）的变化先变大再变小，在中间某个波长值时，辐射曲线会出现一个顶峰，该波长的电磁波辐射能力达到最大值。这个顶峰所对应的波长，被称为λmax，而且物体的温度升高，这个能力巅峰会向着波长变小（频率变高）的方向移动。即横轴为波长的话，顶峰是向左移动的。如下图所示。

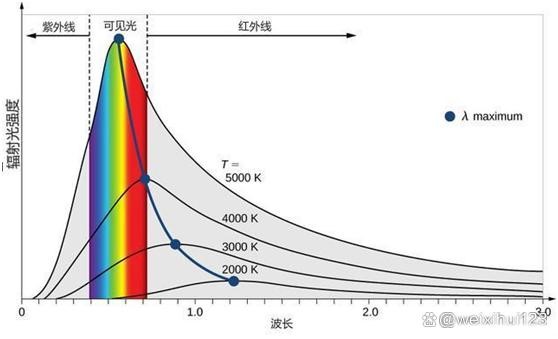
至于为什么两边低中间高，为什么最高点会随着温度增加向频率更高的方向移动？真相很简单，后面会一一揭示。这不是问题的关键。至少目前不是。

问题的关键是，随着辐射计的改进，精度的提高，维恩公式在长波区域与实验所测得的数据不符合了。实验值（下图黑点）高于维恩公式的计算值（维恩线），如下图所示。

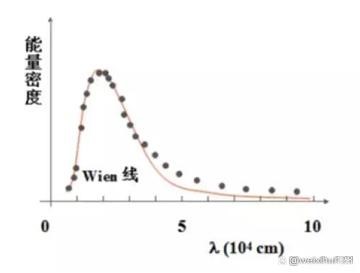
对于维恩公式，一般这样描述“维恩公式在短波段符合，在长波段不符合”。但从客观来看，将其定性为不符合是夸大其实了，应该是“在长波段与实验值有所偏差”。

实验曲线和维恩曲线这两条曲线在长波段呈现规律性的并行延伸。我并不是在为维恩辩护，这是一个客观事实。

长波电磁波包含红外光、微波、无线电波，是能量较弱的电磁波。 可以通俗理解为极微弱的光。

关于辐射曲线在长波波段不符合这件事，为了便于理解，打一个很浅显的比喻，这就像一个石头被炸碎，飞出去有大石、中石、小石子、粉尘。大中小这些石块很符合之前统计的分布规律，但是对于极微小的粉尘，不符合，实际收集到的粉尘，要比理论计算的粉尘，要多。

实际收集的量，比理论计算的量，要大，而且总是稍大那么一点点。

那么，这个问题如何解决？普朗克教授利用插值法对维恩公式做了稍微的修正，在维恩公式框架不变的情况下，只对维恩公式的分母做了一个小小的改动，将分母-1，减一。如下图所示。上面是维恩公式，下面是普朗克公式

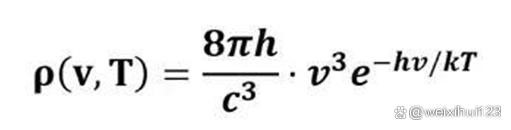
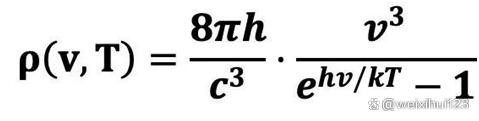
这就导致了当分母比较大时，-1几乎对结果没有影响，而在分母变得很小后，减一将会使得结果明显提高。

举个例子，当分母为一万时，1/10000与1/9999没什么差异，分母较小时，比如1/4变成 1/3，后者有了明显的提高。

这也就导致当频率较高，分母较大时，修正后的数值几乎不变，而频率较低（波长较长）分母较小时，数值明显增大。

最终的结果就是，普朗克曲线与维恩曲线相比，前面的曲线几乎没动，后面的曲线有了显著的抬升。这样，实验值就与理论值（普朗克公式）符合了。

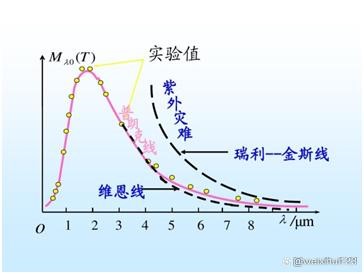
这不是一次伟大的创新，理论的颠覆，这更像是一次微创新，或者一个数学技巧。

这是客观事实，也是一个很简单的数学改变，仔细想想就能想通。

有人说普朗克公式在短波波段和长波波段，公式与实验数据都符合，这是很了不起的。实际上，这并不意外，这是理所当然，因为所谓内插法、插值法，就是拿已经测出的实验结果不断地去尝试，是从结果倒推出了一个公式。这个公式当然会与结果符合。

其实你也可以去试，你要对维恩公式做一次修正，要将分母减去一个数值，但你完全没有眉目，那就把这个数值范围放大一些，比如0-10000，把现有实验数据带进去，结果10000太大，那就减半，试5000，5000还是偏大，那再减半，试2500,这样二分之一递减的话用不了十几次就可以把1试出来。

实际上，-1并不是完全符合的！如上图所示（粉红曲线与黄色圈点并未完全重合）。只是相对于维恩公式来说更符合。这个数值依然有精进的空间，假设这个区间继续缩小，缩小到1.0-1.05之间，再尝试中间值1.025，发现这个数值仍偏大，这样区间就缩小到了1.0-1.025之间，以此类推，再再缩小到1.0125-1.0250间，如果，我是说如果，也用内插法推出一个数值1.0134，比普朗克公式的1更符合，那么能否取代普朗克公式呢？

不能。实验数据与理论公式总有一定的偏差，不能拿前者作为准绳，用来量度公式正确与否。如果把实验数据看做神圣不容置疑的，那就不该有平滑的曲线，又或者各个公式应该根据实验数据做出调整，乘以诸如1.0001之类的修正系数，以做到与实验数据的完全吻合。这是可笑的，是本末倒置。

维恩公式在高频段甚至中频段与实验数据十分契合，这表明这个公式绝非偶然。人们应该去思考，为什么与实验数据符合的很好的维恩公式，到了低频段（长波波段）却与实验值出现了偏差？准确来讲是出现了规律性的少量偏差。人们应该去深入思考去探究原因，而不是减一个修正值了事。

这是轻率的，不负责任的。实际上，普朗克在硬生生凑出这个公式后也陷入了迷惘，因为他要给这个公式、这个-1赋予物理意义，或者说要能从数理上推导出来。这很艰难，甚至他在信中自嘲陷入“绝望”。（如果普朗克将这个数值继续精进，比如1.0082，那才是真正的绝望）

好在，经过长久的努力，分母-1终于有了推导过程，量子力学由此诞生、发展。

准确来讲，量子力学不是起源于瑞利金斯公式，而是起源于维恩公式在长波段出现了偏差。

那么，为什么出现了偏差？人们应该做的是反思，是探究原因，而不是做个-1修正。

其实维恩公式偏差的并不多，并且偏差部分与实验值呈现规律性的并行延伸，下图引自2023年10月23日中科院物理所发表的一篇文章《爱因斯坦对量子假说的初步探索》

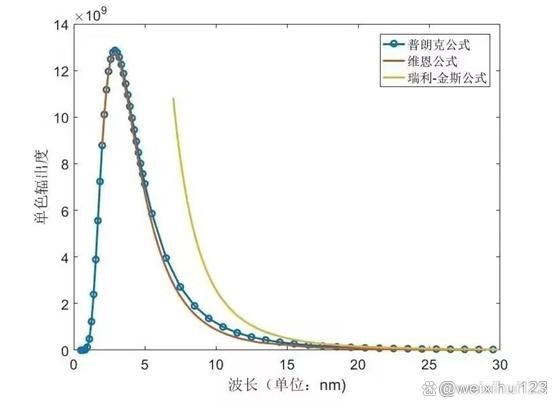
说实话，偏差并不大。维恩公式与大部分实验数据相吻合，契合的非常好，这绝非偶然。我个人认为，维恩公式就是黑体的辐射规律，并不需要减一修正。

那么，为什么在长波区域，实验测量值会高于，准确来讲是稍高于维恩公式的理论值？

这是一个极为重要的问题。它关系着近代物理的走向。

原因很简单，因为室温下其他物体也在辐射长波电磁波，而长波电磁波的穿透性很强，可以穿透各种障碍物，难以隔绝。举个简单的例子，就像电影中经常展示的那样，屋里人们散发的红外辐射，隔着厚厚的混凝土墙体依然可以被屋外的红外夜视仪所接收到。

在黑体辐射实验中，照射进辐射计的长波辐射，除了研究对象黑体的，还多了其他各种物体的长波辐射，测得的数据当然会比理论高一点。

这是一个极其简单的道理。这也是整篇文章的核心。

打个比方，还是将石头爆炸，收集到的其他部分都符合理论推算，但是收集到的粉尘却比理论推算的多，那是因为环境中原本就有一些粉尘啊。做不到净空的条件，搜集到的粉尘数值自然比预想的要多一点。

之所以推出黑体，是为了摈弃外来反射这个干扰因素。但是消除掉外界长波辐射这个干扰因素，受限于当时的认知水平，人们没有想到。当时人们对于电磁波的认知，还处于初级阶段，甚至可以说是萌芽阶段。

那么，如何来验证这一点，很简单，重复黑体辐射实验，作对比，前面复刻实验，后面尽可能的屏蔽外界长波辐射（又或者尽可能的降低实验环境温度，比如贴近绝对零度，以减少其他物体的长波辐射），如果后者的曲线与维恩曲线重合，甚至于不需要重合，只要增加屏蔽之后，曲线有明显的向着维恩曲线贴近的趋势，只要能确认这一点，就能验证猜想，就能得到结论，实验曲线之所谓稍高于维恩曲线，是因为外界的长波干扰，长波摄入。

完全屏蔽外界长波辐射，这个实验条件是十分苛刻的。这里有个简单的验证思路，就是同样的实验条件，白天做和深夜做，对比数据。因为白天多了太阳这个6000K的辐射源，它的长波辐射是个明显且巨大的干扰因素。在同样的实验条件下，如果能确认深夜的数值比白天的低，也可以验证这一点。

这是个简陋又简单的验证实验。

如果维恩公式被证实，普朗克公式被证伪，那么能量量子化的理论就要重申审视了。